Underwater acoustics
Sound is the primary method used for a wide variety of underwater activities, including communication, sonar, navigation, exploration, and monitoring. These activities span a broad spectrum of domains from marine biology and climatology, to defence, navigation, and transport. The earliest recorded use of sonar by humans was in the late 15th century when da Vinci used a partially submerged tube to listen to passing ships. However, we still lack a comprehensive understanding of the complex processes that are involved in the propagation of sound underwater and the mechanisms associated with these phenomena are rarely studied and remain poorly understood, particularly from a mathematical and physical perspective. This project will provide an introduction to some of the methods used to model and study underwater acoustics; the project will involve both analytical and numerical approaches.
Further reading
Whitchelo Y, Haslinger SG, Colquitt DJ, Williams DP. 2023 Scattering of acoustic waves from rough seabeds: a comparison of two- and three-dimensional models. Proc Mtgs Acoust, 8 May 2023, 51(1) : 070003. (doi: 10.1121/2.0001801)
Jensen FB, Kuperman WA, Porter MB, Schmidt H, Tolstoy A. 2011 Computational ocean acoustics. New York: Springer New York.
Brekhovskikh LM, Lysanov YP, Beyer RT. 1991 Fundamentals of ocean acoustics. New York: Springer New York.
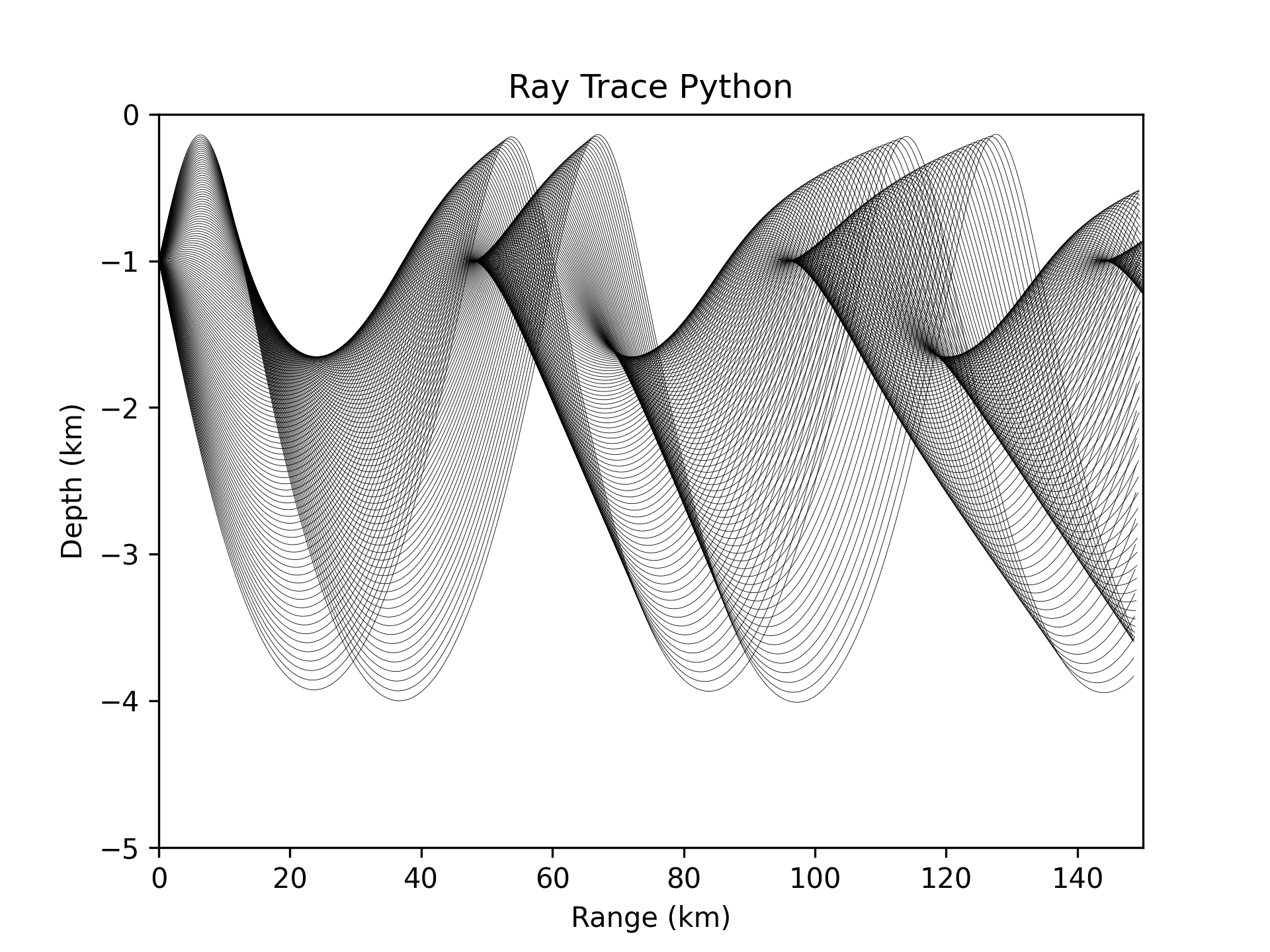
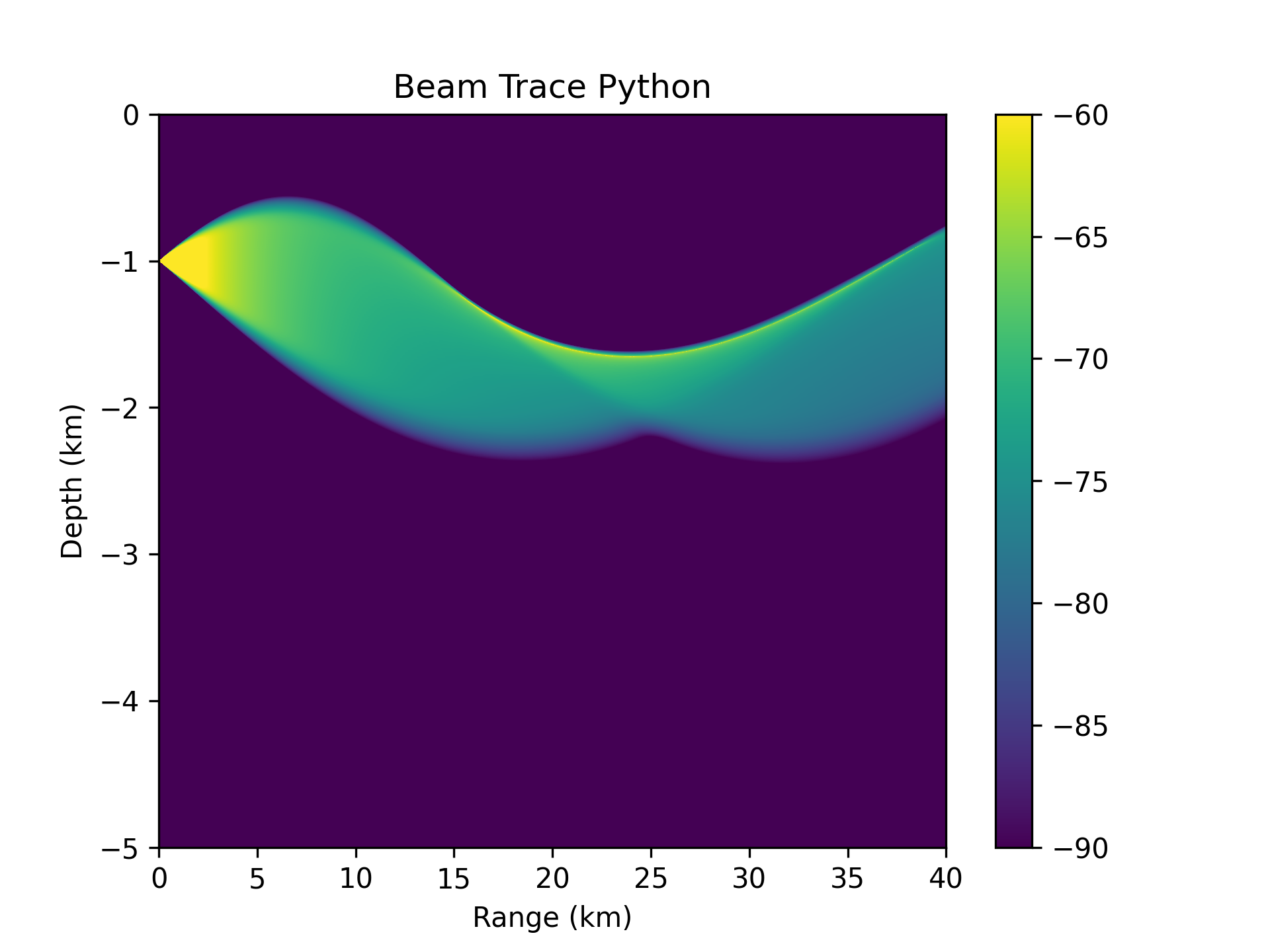

Surface wave control
This project involves the mathematical modelling and design of mechanical structures capable of controlling the propagation of surface and bulk waves in elastic solids. The project will employ both numerical and asymptotic analysis to study a combination of continuous and discrete structures in one-, two-, and three-dimensions. The research programme includes scattering, homogenisation, and spectral problems for finite and infinite systems and has a broad range of applications including, filtering of waves, lensing, and cloaking.
Further reading
Skelton EA, Craster RV, Colombi A, Colquitt DJ. 2018 The multi-physics metawedge: graded arrays on fluid-loaded elastic plates and the mechanical analogues of rainbow trapping and mode conversion.New J Phys, 20, 053017. (doi: 10.1088/1367-2630/aabecf)
Carta G, Colquitt DJ, Movchan NV, Movchan AB, Jones IS. 2020 A new class of chiral flexural waves in structured plates: directional localisation and control.J Mech Phys Solids, 137, 103866 (doi: 10.1016/j.jmps.2020.103866).
Colquitt DJ, Colombi A, Craster RV, Roux P, Guenneau SRL. 2017 Seismic metasurfaces: Sub-wavelength resonators and Rayleigh wave interaction. J Mech Phys Solids, 99, 379-393. (doi: 10.1016/j.jmps.2016.12.004)
Maling BJ, Colquitt DJ, Craster RV. 2017 The homogenisation of Maxwell's equations with applications to photonic crystals and localised waveforms on gratings. Wave Motion, 69, 35-49. (doi: 10.1016/j.wavemoti.2016.11.003)
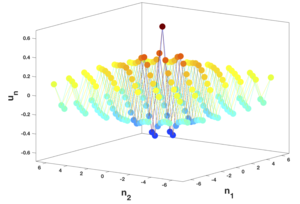
Discrete defects
This project involves the analysis of finite and semi-infinite defects in elastic lattice systems. These defects may be dislocations or variations in inertial properties and, for finite defects, will have an associated spectrum of eigenstates. The focus of the research programme is on the analysis of these eigenstates and the fields in the vicinity of the defect sites; algorithms will be developed to study the solutions in various asymptotic regimes. The research programme will involve both analytical and numerical models. The project may also include the study of edge and interfacial waves in mechanical lattices.
Further reading
Colquitt DJ, Nieves MJ, Jones IS, Movchan AB, Movchan NV. 2013 Localisation for a line defect in an infinite square lattice. Proc. R Soc. A 469 : 20120579. (doi: 10.1098/rspa.2012.0579)
Colquitt DJ, Nieves MJ, Jones IS, Movchan NV, Movchan AB. 2012 Trapping of a crack advancing through an elastic lattice.
Int J Eng Sci 61, 129–141. (doi: 10.1016/j.ijengsci.2012.06.016)
Madine KH, Colquitt DJ. 2021 Dynamic Green's functions in discrete flexural systems. Q J Mech Appl Math, hbab006. (doi: 10.1093/qjmam/hbab006)